
Coterminal and Reference Angles Exercise 4
Finding a coterminal angle along with its reference angle and graphing it
Problem: Find one negative and one positive coterminal angle for \(60^\circ\) and \(\dfrac{\pi}{3}.\)

Finding a coterminal angle along with its reference angle and graphing it

Finding a coterminal angle along with its reference angle and graphing it

Defining coterminal angles and how to determine if angles are coterminal

Drawing an angle in standard position and finding its reference angle

Drawing an angle in standard position and finding its reference angle

Drawing an angle in standard position

How to find reference angles for angles in standard position

Discussing the degree and radian measure of special angles on the unit circle

The coordinates for the quadrantal angles on the unit circle

Finding the coordinates on the unit circle for the common angles in the first quadrant

Finding the angle where secant has a given value and tangent is positive

Finding the exact values of sine and secant for several given angles using the unit circle

Defining radians for angle measure using the corresponding arc length on a unit circle

Converting an angle measured in degrees to radians

Converting angles measured in radians to degrees

Finding the radius of a circle using the area of a sector

Finding a vector given its length and angle with the positive x-axis

Tangent lines to parametric equations and related rates examples

Review of limits and derivatives of inverse trigonometric functions
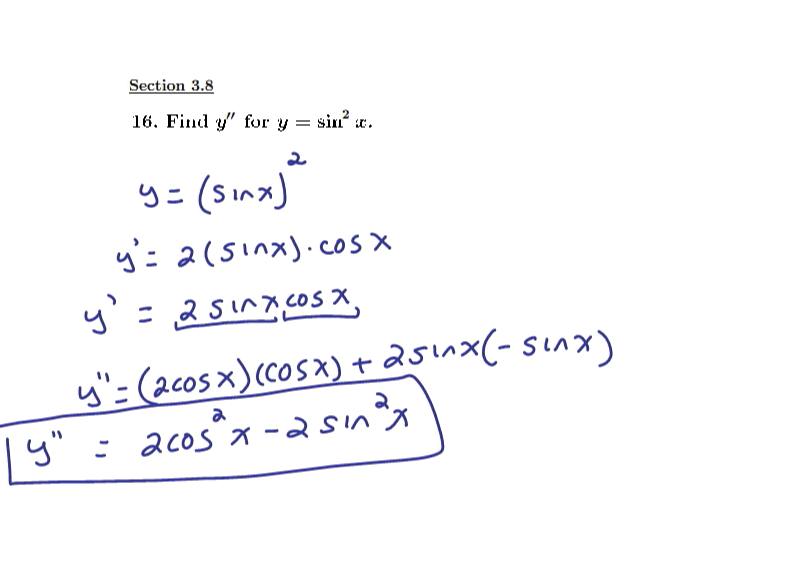
Derivatives of parametric equations and tangent lines

Review of limits and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Tangent lines to parametric equations and related rates examples

Find the measure of an angle given the three vertices for the angle

Determining the rate that the area of a triangle is increasing based on the rate an angle is increasing

Tangent lines to parametric equations and related rates examples

Review of limits and derivatives of inverse trigonometric functions
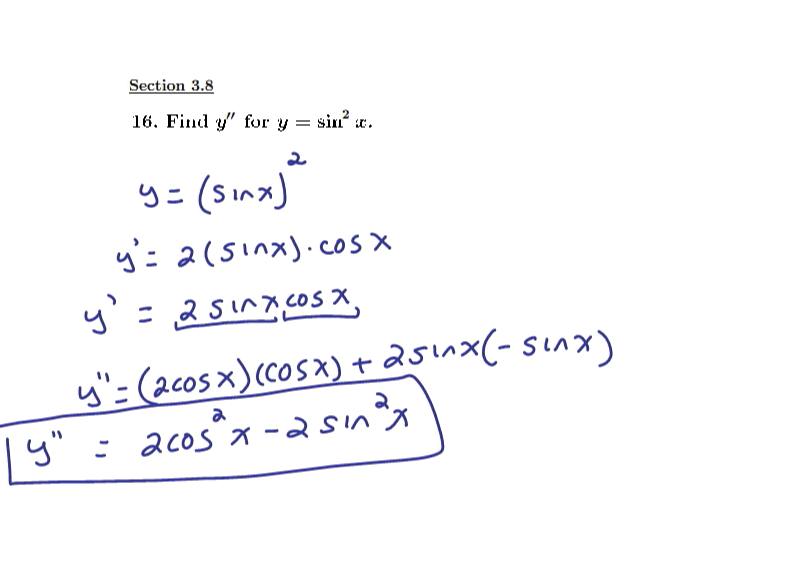
Derivatives of parametric equations and tangent lines

Review of limits and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Tangent lines to parametric equations and related rates examples

Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent

Finding the six trigonometric ratios for a right triangle

Using trig to find the length of the side of a right triangle given an angle and side length

Using trig to find an angle in a right triangle with two given sides

Explaining the Pythagorean Theorem and using it to find a missing side in a right triangle

Explaining the special right triangles and the relationships between their sides

Special Right Triangles Exercise 1

Special Right Triangles Exercise 2

Finding the coordinates on the unit circle for all the common angles

Finding the values of trig functions with the unit circle

Finding the exact value of tangent for several given angles using the unit circle

Finding the exact value of secant, cosecant, and cotangent using the unit circle

Finding the exact values of cosine and cotangent for given angles using the unit circle

Finding the angles where sine has a given value using the unit circle

Using the unit circle to sketch the graph of the sine function

Using the unit circle to sketch the graph of the cosine function

Using the unit circle to sketch the graph of the tangent function

Graphing the reciprocal trig functions cosecant, secant, and cotangent

Graphing a period of a transformed sine function

Graphing a period of a transformed cosine function

Writing the sine and cosine functions for a given graph

Using the reciprocal and ratio trig identities to simplify an expression

Using the Pythagorean Identities to simplify a trig expression

Using the Pythagorean Trig Identity to derive the secondary Pythagorean Identities

Using the sum identities of sine and cosine to derive the double angle identities

Using the difference identities of sine and cosine to derive the cofunction identities

Using the double angle identities for cosein to derive the half-angle identities for sine and cosine

Using the Sum and Difference Identities to find the exact value of cosine

Using the Sum Identity for Trig to find the exact value of sine

Using a Double Angle Identity to find the exact value of an expression with sine and cosine

Using the Half-Angle Identities to find the exact values of sine, cosine, and tangent

Using the Reciprocal, Ratio, and Pythagorean Identities to verify a trig identity

Proving a trigonometric identity involving secant, cotangent, and tangent

Proving a trig identity involving sine and cosine

Proving a trig identity involving sine, cosine, and cotangent

Finding all solutions to a trigonometric equation with sine

Solving a trigonometric equation with sine and cosine by factoring

Solving a trigonometric equation with secant by factoring

Solving a trigonometric equation with tangent and sine by factoring

Using the Even/Odd and Cofunction Identities to solve an equation with sine

Solving a trig equation with sine and cosine using aPythagorean Identity

Solving a trig equation with cotangent and cosecant using trig identities

Solving a trig equation with sine and tangent using a trig identity

Solving a trig equation with sine and cosine using trig identities

Solving a trig equation with cosine using trig identities

Solving a trig equation with cotangent and sine using trig identities

Using trigonometry to determine the edge lengths of a right triangle

Evaluating trigonometric functions given a point on the terminal side of an angle

Evaluating trigonometric functions given a point on the terminal side of an angle

Finding trigonometric functions given information about the angle

Evaluating all six trigonometric functions for a right triangle

Evaluating all six trigonometric functions for a right triangle

Using trigonometry to determine the height of a tree