
Solving Trig Equations Using Identities Exercise 2
Solving a trig equation with sine and cosine using aPythagorean Identity
Problem: Solve \(2\sin{x}\cos{x} = \sqrt{2}\cos{x}\) for \(0\leq x \leq 2\pi.\)
Solution: \(x=\dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3\pi}{4},\dfrac{3\pi}{2}\)
Solution Method: A tempting first step here is to divide by a \(\cos{x}\) on both sides. But if we do that, we’ll be losing a solution to the equation! (Think about \(x^2=3x\). We can clearly see that \(x=0\) is a solution to the equation. But if we divide by x, we may think \(x=3\) is the only solution.)
So instead of dividing by \(\cos{x}\) as out first step, we’re going to move everything over to one side and set it equal to zero. \[\begin{aligned} 2\sin{x}\cos{x} &= \sqrt{2}\cos{x} \\ 2\sin{x}\cos{x} - \sqrt{2}\cos{x} &= 0 \end{aligned}\] Then I can factor out a \(\cos{x}\), \[\begin{aligned} 2\sin{x}\cos{x} - \sqrt{2}\cos{x} &= 0 \\ \cos{x}(2\sin{x} - \sqrt{2}) &= 0 \end{aligned}\] So I have two factors I can set equal to 0 and solve for x.
2 \[\begin{aligned} \cos{x} = 0 \end{aligned}\] Zero is a quadrantal value and thinking back to the unit circle, I know \(x=\frac{\pi}{2}, \frac{3\pi}{2}\) satisfy \(\cos{x}=0\). \[\begin{aligned} 2\sin{x}-\sqrt{2} &= 0 \\ 2\sin{x} = \sqrt{2} \\ \sin{x} = \frac{\sqrt{2}}{2} \end{aligned}\] The reference angle that produces sine equal to \(\frac{\sqrt{2}}{2}\) is \(\frac{\pi}{4}\). The sine value is also positive, so I’m in Q1 or Q2 (by ASTC). So the x values satisfying the equation are \(x=\frac{\pi}{4}, \frac{3\pi}{4}\).
So we have a total of four x-values satisfying \(2\sin{x}\cos{x} = \sqrt{2}\cos{x}\), \(x=\frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4}, \frac{3\pi}{2}.\)

Solving a trig equation with sine and cosine using aPythagorean Identity

Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent

Finding the values of trig functions with the unit circle

Using the unit circle to sketch the graph of the tangent function

Graphing the reciprocal trig functions cosecant, secant, and cotangent

Writing the sine and cosine functions for a given graph

Using the sum identities of sine and cosine to derive the double angle identities

Using the difference identities of sine and cosine to derive the cofunction identities

Using a Double Angle Identity to find the exact value of an expression with sine and cosine

Using the Half-Angle Identities to find the exact values of sine, cosine, and tangent

Solving a trigonometric equation with tangent and sine by factoring

Finding all solutions to a trigonometric equation with sine

Solving a trig equation with sine and cosine using trig identities

Solving a limit example with a trigonometric functions

Solving a limit example with a trigonometric function

Evaluating a trigonometric limit using trigonometric identities

Evaluating compositions with inverse trigonometric functions

Evaluating compositions with inverse trigonometric functions

Verifying a trigonometric identity

Verifying a trigonometric identity

Solving a trigonometric equation by factoring

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using double angle formulas to evaluate trigonometric functions

Using a sum formula to rewrite a trigonometric expression

Properties and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Finding a Cartesian equation for a parametric curve

Using vectors to find the magnitude and direction of a resultant force

Evaluating compositions of trigonometric and inverse trigonometric functions

Converting parametric equations into a Cartesian equation

Converting parametric equations into a Cartesian equation and graphing

Using trigonometric identities to integrate powers of sine and cosine

Integrating a function with sine using u-substitution

Proving facts about the derivatives of vector functions including the product rule

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Proving the derivatives of trigonometric functions and that sine is continuous

Properties and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Using u substitution to evaluate integrals and prove facts about logarithms and integrals and

Interpreting integrals to represent areas between curves

Proving trigonometric identities useful for integration

Using trigonometric identities to integrate powers of sine and cosine

Finding a partial fraction decomposition and integrating using partial fractions

Using a rotation map matrix to rotate a 2-dimensional vector by the angle \(\pi\)

Using trig to find an angle in a right triangle with two given sides

Finding the exact values of cosine and cotangent for given angles using the unit circle

Finding the exact values of sine and secant for several given angles using the unit circle

Finding the angles where sine has a given value using the unit circle

Finding the angle where secant has a given value and tangent is positive

Using the unit circle to sketch the graph of the sine function

Using the unit circle to sketch the graph of the cosine function

Graphing a period of a transformed sine function

Graphing a period of a transformed cosine function

Using the double angle identities for cosein to derive the half-angle identities for sine and cosine

Using the Sum and Difference Identities to find the exact value of cosine

Using the Sum Identity for Trig to find the exact value of sine

Solving a trigonometric equation with secant by factoring

Solving a trig equation with cosine using trig identities

Solving a trig equation with sine and tangent using a trig identity

Using trigonometry to determine the edge lengths of a right triangle

Evaluating trigonometric functions given a point on the terminal side of an angle

Evaluating trigonometric functions given a point on the terminal side of an angle

Evaluating all six trigonometric functions for angles in degrees and radians

Evaluating all six trigonometric functions for a right triangle

Evaluating all six trigonometric functions for a right triangle

Finding the values of all six trigonometric functions of an angle given a right triangle

Evaluating the other five trigonometric functions for an acute angle given the value of sine

Evaluating the other five trigonometric functions given sine and that tangent is negative

Solving a trigonometric equation with sine and cosine on a given interval

Solving an quadratic-like equation with sine by factoring

Determining the properties of a sine function and graphing it

Writing the equation for a sine function with certain characteristics

Determining the properties of a cosine function and graphing it

Writing the equation for a cossine function with certain characteristics

Writing the equation for a sine function to match a given graph

Writing the equation for a cosine function to match a given graph

Evaluating a composition of trigonometric and inverse trigonometric functions

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Using a difference formula to evaluate a trigonometric function

Using a sum formula to evaluate a trigonometric expression

Using the Law of Sines to solve a triangle

Using the Law of Sines to solve a triangle

Using the Law of Cosines to solve a triangle

Using the Law of Sines to solve a triangle

Cartesian equations and parametric equations of curves

Tangent lines to parametric equations and related rates examples
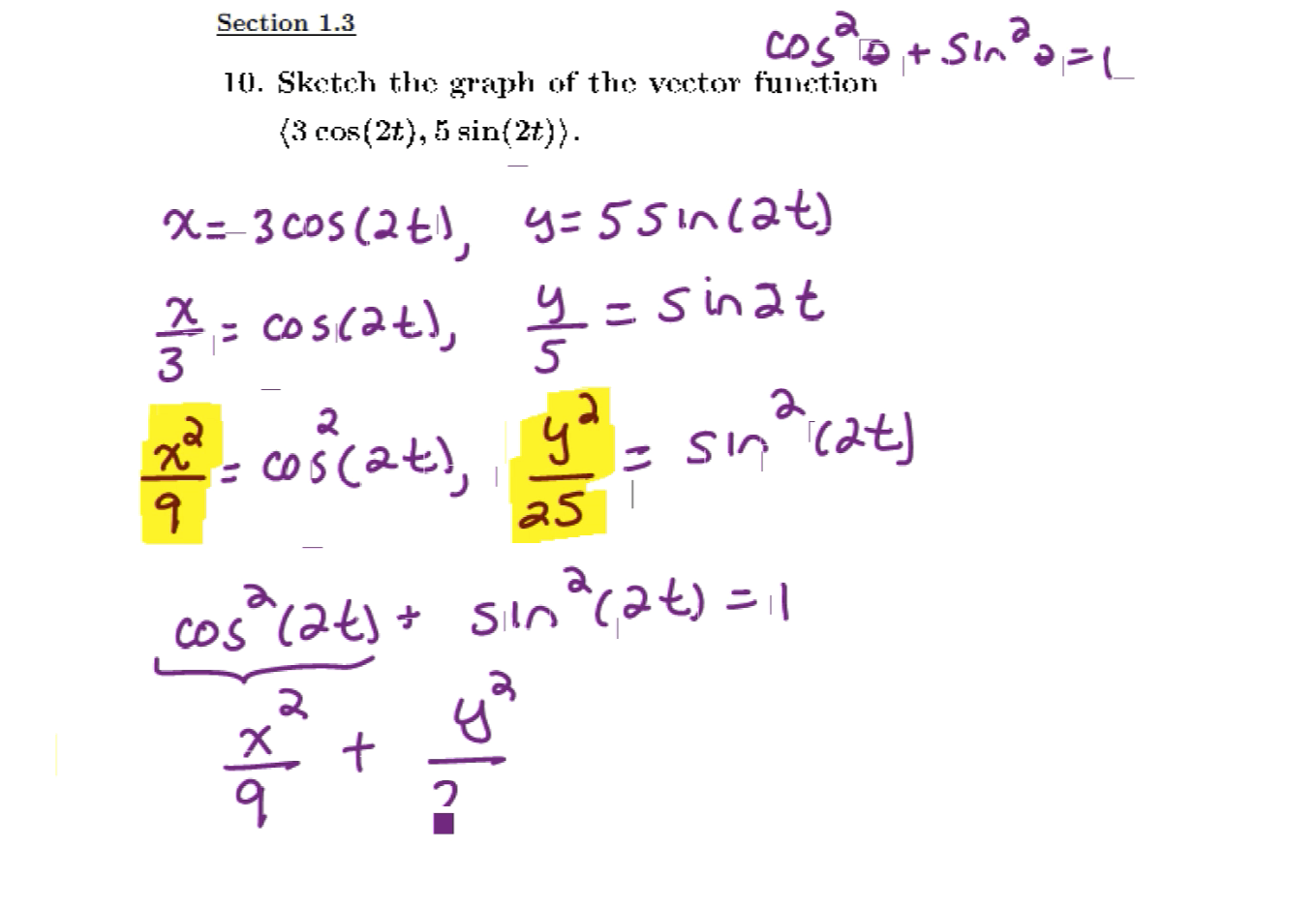
Review of vector functions and parametric equations

Review of limits and derivatives of inverse trigonometric functions
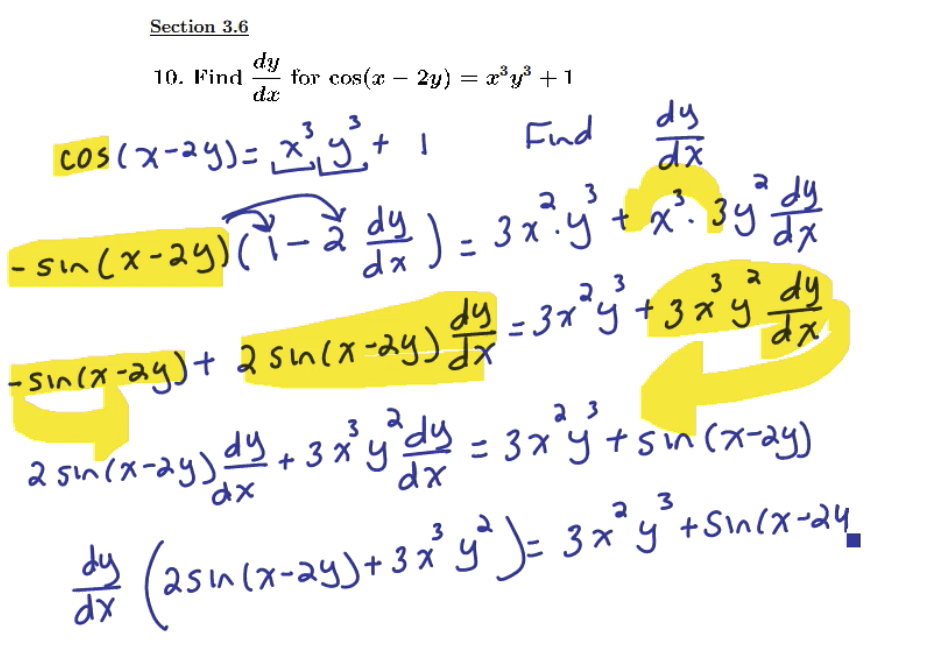
Implicit differentiation and physics applications of derivatives
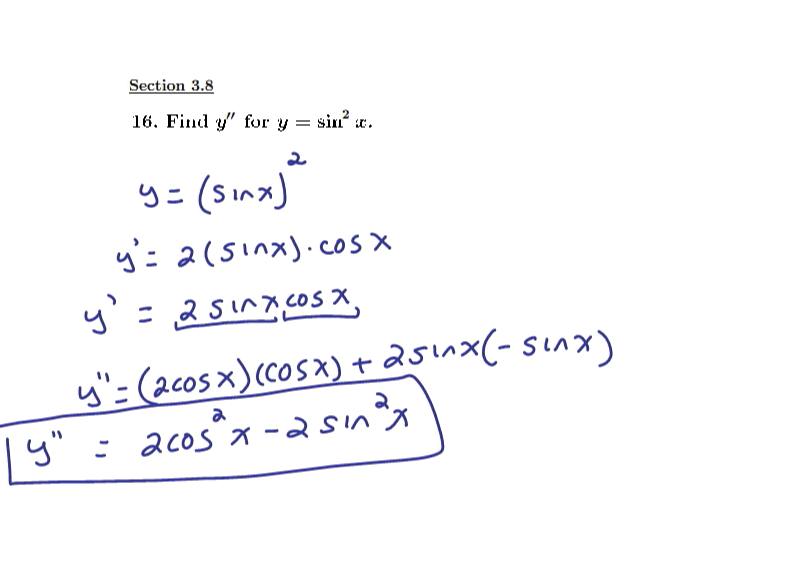
Derivatives of parametric equations and tangent lines

Reviewing the chain rule and the derivatives and limits of trigonometric functions

Review of limits and derivatives of inverse trigonometric functions

Derivatives of trigonometric functions and using the Chain Rule

Derivatives of trigonometric functions and using the Chain Rule

Implicit differentiation and finding tangent lines

Derivatives of exponential and logarithmic functions and the exponential model

Derivatives of exponential and logarithmic functions and the exponential model

Tangent lines to parametric equations and related rates examples

Mean Value Theorem and properties of a graph

Mean Value Theorem and properties of a graph

Using Reimann sums and the Fundamental Theorem of Calculus

Using Riemann sums and the Fundamental Theorem of Calculus

Evaluating a composition of trigonometric and inverse trigonometric functions

Simplifying expressions containing trigonometric and inverse trigonometric functions

Using the Chain Rule to differentiate functions

Using the Chain Rule to differentiate functions with exponential and trigonometric functions

Using the Chain Rule to differentiate a function containing trigonometric functions

Using the Chain Rule to find the pattern for a higher order derivative

Finding the derivative using implicit differentiation

Finding the derivative using implicit differentiation

Finding the derivative using implicit differentiation

Finding the derivative using implicit differentiation
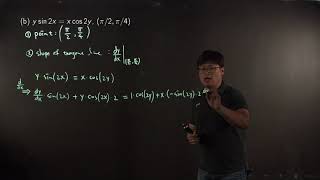
Finding a tangent line to an curve defined implicitly

Finding the derivative of a function containing a logarithmic function

Finding the derivatives of functions containing logarithms

Finding the derivative of a function containing a logarithms

Using logarithmic differentiation to find the derivative of a function

Using logarithmic differentiation to find the derivative of a function

Graphing a vector function by converting it to a Cartesian equation

Finding the tangent line to a parametric curve

Using the chain rule to find a derivative

Using logarithmic differentiation to find the derivative of a function

Using logarithmic differentiation to find the derivative of a function

Finding where a function has horizontal tangent lines

Finding a higher order derivative of a function

Using the Quotient and Chain Rules to find several derivatives

Using the Product and Chain Rules to differentiate functions with logarithms

Differentiating functions with logarithmic and inverse trigonometric functions

Using the Product and Chain Rule to find several derivatives

Finding the absolute maximum and absolute minimum values of a function on a closed interval

Evaluating a limit using L'Hospital's Rule

Finding the antiderivative of a function

Finding a function from its second derivative using antidifferentiation

Antidifferentiating twice to find a function from its second derivative

Antidifferentiating twice to find a function from its second derivative

Antidifferentiating to find a function from its derivative

Antidifferentiating twice to find a function from its second derivative

Evaluating a limit with an indeterminant product using L'Hospital's Rule

Finding the antiderivative of a function and using a function value to find the constant

Finding the derivative of an implicit function

Finding the derivative of an implicit function

Determining the rate that the area of a triangle is increasing based on the rate an angle is increasing

Using L'Hospital's Rule to solve a limit

Using the Fundamental Theorem of Calculus to find the derivative of a function defined using an integral

Evaluating a definite integral with an exponential and sine function

Using u-substitution to evaluate an indefinite integral

Review of sequences and finding the sum of a series

Review of trigonometric substitution

Review of Taylor and Maclaurin Series and their properties

Converting parametric equations into a Cartesian equation and graphing

Find the integral representing the surface area of a rotated parametric curve

Finding Taylor and Maclaurin Series for functions

Using trigonometric identities to solve an integral with powers of sine and cosine

Using trigonometric identities to integrate a power of cosine

Using a trigonometric identity to integrate powers of sine and cosine

Using a trigonometric identity to integrate powers of sine and cosine

Using trigonometric identities to integrate even powers of sine and cosine

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Using u-substitution on an indefinite integral with an exponential function, sine, and cosine

Cartesian equations and parametric equations of curves

Calculating slopes of tangent lines to parametric curves

Tangent lines to parametric equations and related rates examples
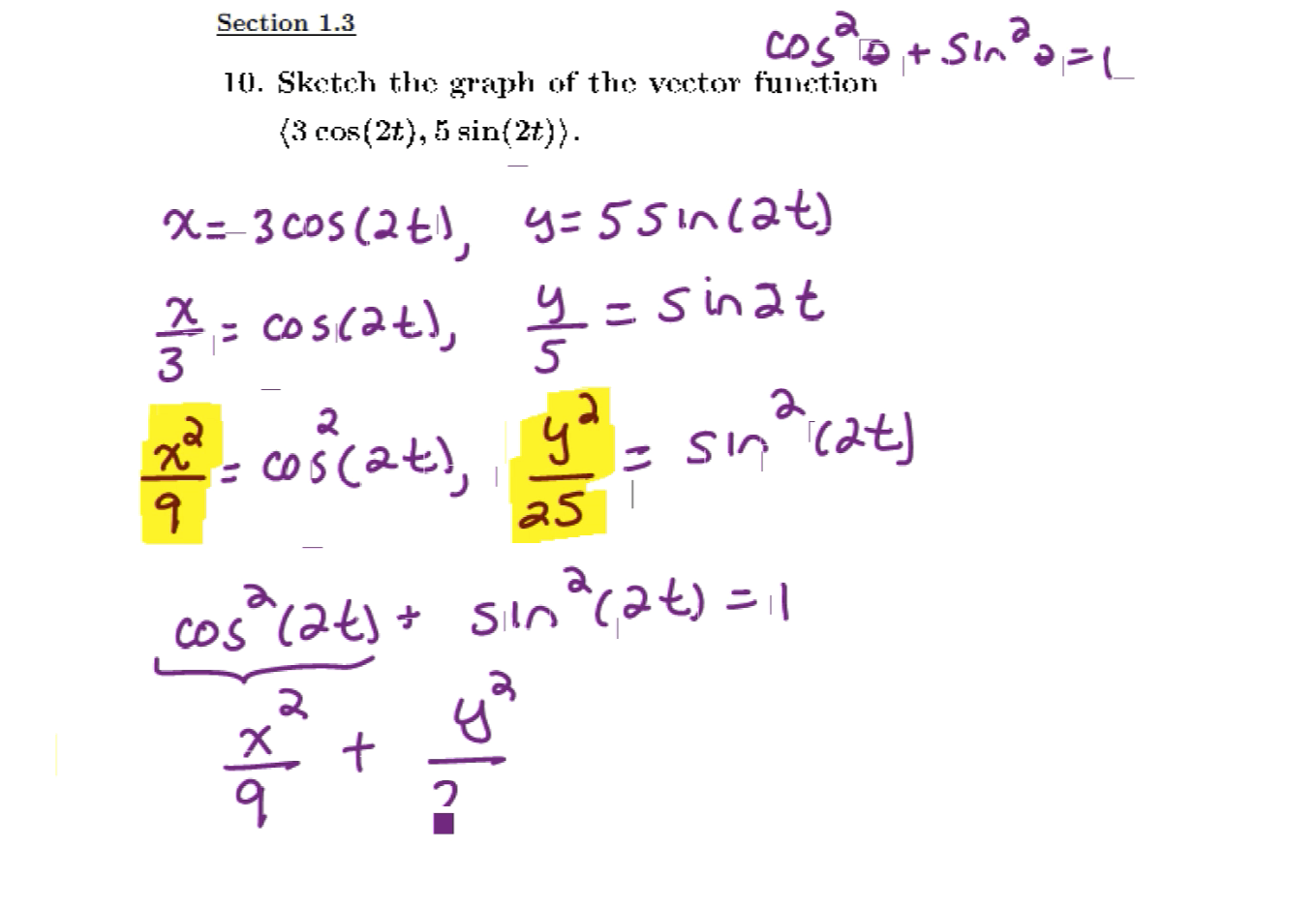
Review of vector functions and parametric equations

Review of limits and derivatives of inverse trigonometric functions
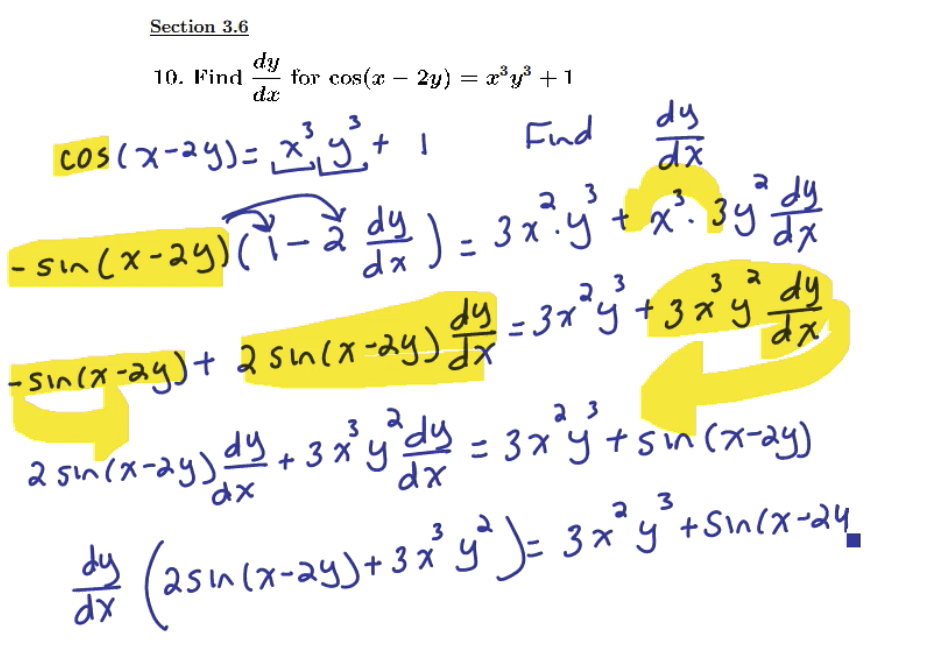
Implicit differentiation and physics applications of derivatives
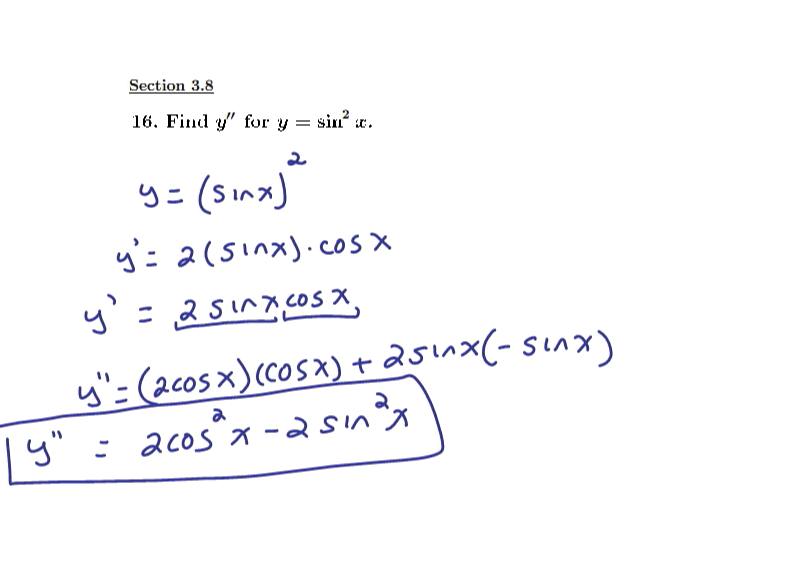
Derivatives of parametric equations and tangent lines

Reviewing the chain rule and the derivatives and limits of trigonometric functions

Review of limits and derivatives of inverse trigonometric functions

Proving a property of scalar multiplication for limits using the epsilon-delta definition and using the Squeeze Theorem for Limits.

Derivatives of trigonometric functions and using the Chain Rule

Examples involving the tangent line to an exponential function and finding the derivative of hyperbolic cosine

Derivatives of trigonometric functions and using the Chain Rule

Implicit differentiation and finding tangent lines

Derivatives of exponential and logarithmic functions and the exponential model

Tangent lines to parametric equations and related rates examples

Mean Value Theorem and properties of a graph

Mean Value Theorem and properties of a graph

Using Reimann sums and the Fundamental Theorem of Calculus

Using Reimann sums and the Fundamental Theorem of Calculus

Review of sequences and finding the sum of a series

Review of trigonometric substitution

Review of Taylor and Maclaurin Series and their properties

Finding Taylor and Maclaurin Series for functions

Reviewing Taylor and Maclaurin Series and Taylor's Inequality

Integrating using a trigonometric substitution

Finding the limit of a three-dimensional vector function

Finding the angle of intersection for two three-dimensional vector functions

Finding the length of a three-dimensional curve

Finding the position vector function given the velocity and an initial position

Finding all second-order partial derivatives of a function of two variables

Finding the maximum rate of change and the direction it occurs for a function of two variables

Evaluating a double integral over a rectangle

Evaluating a double integral by changing to polar coordinates

Evaluating a double integral by changing to polar coordinates

Using an iterated integral in spherical coordinates to find the volume of a solid

Evaluating a triple integral for a given solid by writing an iterated integral in spherical coordinates

Evaluating a line integral along half a circle

Evaluating a line integral of a vector field along an curve

Using Green's Theorem to evaluate a line integral on a closed curve

Evaluating a surface integral over a cylinder

Finding the six trigonometric ratios for a right triangle

Using trig to find the length of the side of a right triangle given an angle and side length

Explaining the special right triangles and the relationships between their sides

Finding the exact value of tangent for several given angles using the unit circle

Finding the exact value of secant, cosecant, and cotangent using the unit circle

Using the reciprocal and ratio trig identities to simplify an expression

Using the Pythagorean Identities to simplify a trig expression

Using the Pythagorean Trig Identity to derive the secondary Pythagorean Identities

Using the Reciprocal, Ratio, and Pythagorean Identities to verify a trig identity

Proving a trigonometric identity involving secant, cotangent, and tangent

Proving a trig identity involving sine and cosine

Proving a trig identity involving sine, cosine, and cotangent

Solving a trig equation with cotangent and sine using trig identities

Using the Even/Odd and Cofunction Identities to solve an equation with sine

Solving a trig equation with cotangent and cosecant using trig identities

Finding trigonometric functions given information about the angle

Solving an equation with cosine on a given interval

Solving a trigonometric equation with sine on a given interval

Sketching one period of a transformed sine graph

Finding the amplitude, period, phase shift, and vertical shift for a given sine function

Writing a cosine function for a given graph

Determining if a series converges or diverges

Solving an equation with exponential functions

Subtracting rational functions and then simplifying the result

Multiplying two rational functions and simplifying the result

Dividing rational functions and simplifying the result

Dividing and subtraction rational functions and simplifying the result

Finding the difference quotient for a quadratic function

Factoring an algebraic expression

Factoring a quadratic

Factoring a polynomial

Factoring a quadratic

Dividing rational expressions and simplifying

Subtracting rational expressions and simplifying

Performing operations with rational expressions and simplifying

Performing operations with rational expressions and simplifying

Solving a polynomial equation using factoring by grouping

Finding the x-intercepts of quadratic functions

Finding properties of a polynomial including zeros and end behavior

Finding properties of a polynomial including zeros and end behavior

Finding properties of a polynomial including zeros and end behavior

Using properties of a polynomial to find its graph

Solving a nonlinear inequality

Solving a nonlinear inequality

Solving a nonlinear inequality

Solving a nonlinear inequality

Solving an equation with exponential functions by factoring

Writing an equivalent algebraic expression for compositions with inverse trigonometric functions containing variables

Using inverse trigonometry to write an expression for an angle in a right triangle

Solving a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a sum formula to evaluate a trigonometric expression

Finding a vector given its length and angle with the positive x-axis

Finding the angle between two vectors

Finding the properties of a transformed tangent function and graphing it

Derivatives and vectors with some physics applications

Derivatives of exponential functions and the exponential model

Mean Value Theorem and using derivatives to find the shape of curves

Antiderivatives and physics applications

Differentials, linear approximations and quadratic approximations

Derivatives and vectors with some physics applications

Derivatives and vectors with some physics applications

Using L'Hospital's Rule to solve limits

Riemann sums, including approximating areas under curves.

Examples of integration by substitution

Calculating the work done pushing a crate up a ramp

Find the measure of an angle given the three vertices for the angle

Using the Product, Quotient and Chain Rules to find several derivatives

Differentiating functions with inverse trigonometric functions

Finding the derivative of an implicit function

Finding the derivative of an implicit function

Antidifferentiating twice to find a function from its second derivative

Using antidifferentiation to find the height of a cliff from the impact speed of a dropped stone

Using u-substitution to evaluate an indefinite integral

Calculating a composition of tangent and arcsine

Finding the length of a curve given by parametric equations

Finding the area of a region defined using polar coordinates

Finding the area of a region defined using polar coordinates

Finding the area of a region defined using polar coordinates

Finding the Maclaurin series of a function

Evaluating a definite integral by rewriting the integrand as its Maclaurin series

Determining if a series is absolutely convergent, conditionally convergent, or divergent.

Evaluating an integral using integration by parts

Evaluating an integral using integration by parts

Solving an indefinite integral with cosine using integration by parts

Using integration by parts twice for an integral with sine and an exponential function

Using trigonometric identities to integrate powers of secant and tangent

Evaluating an integral using trigonometric identities

Using a trigonometric identity to integrate an even power of cosine

Using trigonometric identities to integrate powers of cosine and tangent

Explaining the cases for using trigonometric substitution

Proofs of the Cauchy-Schwarz Inequality and a property of vector projections

Derivatives and vectors with some physics applications

Derivatives and vectors with some physics applications

Derivatives of exponential functions and the exponential model

Mean Value Theorem and using derivatives to find the shape of curves

Antiderivatives and physics applications

Differentials, linear approximations, and quadratic approximations

Derivatives and vectors with some physics applications

Using the Chain Rule to prove facts about derivatives

Using L'Hospital's Rule to solve limits

Riemann sums, including approximating areas under curves.

Examples of integration by substitution

Using trigonometric identities to integrate powers of secant and tangent

Explaining the cases for using trigonometric substitution

Calculating the length of the cross product of two vectors given information about the vectors

Finding a vector equation for the tangent line to a three-dimensional vector function

Finding the partial derivatives of a function of two variables

Finding the partial derivatives of a function of three variables

Converting a double integral to a double integral in polar coordinates

Finding the curl and divergence of a three dimensional vector field

Using the Divergence Theorem to evaluate the surface integral of a vector field

Explaining the Pythagorean Theorem and using it to find a missing side in a right triangle

Special Right Triangles Exercise 1

Special Right Triangles Exercise 2

Discussing the degree and radian measure of special angles on the unit circle

The coordinates for the quadrantal angles on the unit circle

Finding the coordinates on the unit circle for the common angles in the first quadrant

Finding the coordinates on the unit circle for all the common angles

Defining radians for angle measure using the corresponding arc length on a unit circle

Converting an angle measured in degrees to radians

Converting angles measured in radians to degrees

How to find reference angles for angles in standard position

Defining coterminal angles and how to determine if angles are coterminal

Drawing an angle in standard position

Finding a negative and positive coterminal angle for a given angle

Drawing an angle in standard position and finding its reference angle

Drawing an angle in standard position and finding its reference angle

Finding a coterminal angle along with its reference angle and graphing it

Finding a coterminal angle along with its reference angle and graphing it

Finding the values of \(\theta\) that makes a matrix with trig functions invertible

Determining whether trigonometric functions are linearly independent

Finding the dimension of the subspace spanned by a set of functions

Solving a rational equation and checking the solutions

Solving an equation with logarithmic functions

Solving an equation with logarithmic functions

Solving an equation with logarithmic functions

Using trigonometry to determine the height of a tree

Factoring a quadratic polynomial

Factoring a quadratic function

Factoring a cubic polynomial by grouping

Finding the greatest common factor of a polynomial and then factoring it out

Factoring a quadratic where the leading coefficient is 1

Factoring quadratics where the leading coefficient is not 1

Factoring several polynomials by grouping

Factoring a difference of two squares

Factoring a sum of cubes and a difference of cubes

Simplifying a rational expression

Adding and then simplifying two rational expressions

Multiplying two rational expressions and then simplifying

Dividing rational expressions and then simplifying the answer

Adding two rational expressions and then simplifying the answer

Finding any holes, vertical asymptotes, and horizontal asymptotes of a rational function

Finding any holes, vertical asymptotes, and horizontal asymptotes of a rational function

Matching a rational function with its graph

Finding the roots of a square root function

Finding the domain of a function with a quadratic inside a square root

Solving an inequality with a polynomial by factoring and using a sign diagram

Solving an inequality with a rational expression by factoring and using a sign diagram

Solving an inequality with two rational expressions using a sign diagram

Solving an inequality with a rational expression using a sign diagram

Solving an inequality with a quadratic by factoring and using a sign diagram

Solving an equation with exponential functions by factoring

Solving a equation with exponential functions by factoring

Evaluating a composition of tangent and arccosine

Finding the solutions to an equation with tangent in a given interval

Sketching one period of a cosine function with transformations

Using the comparison test to determine if a series converges or diverges

Using the comparison test to determine if a series converges or diverges

Using the limit comparison test to determine if a series converges or diverges

Using the Alternating Series Test to determine if a series converges or diverges

Using the Alternating Series Test to determine if a series converges or diverges

Using the Alternating Series Test to determine if a series converges or diverges

Creating symbolic expression in Python and then factoring, expanding, and simplifying the expressions

Solving equations symbolically in Python and interpreting the results

Using Python to numerically, graphically, and analytically find the limit of a sequence
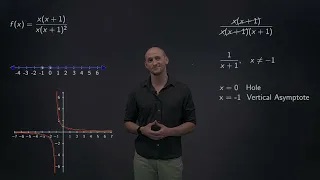
Finding the domain of a rational function using factoring

Finding the domain of a function with a natural logarithm and denominator

Explaining the standard form for a quadratic equation and the possible number of solutions

Solving quadratic equations with the difference of two squares formula

Solving quadratic equations by factoring

Solving a quadratic equation by factoring

Solving a quadratic equation by factoring

Solving quadratic equations with the quadratic formula and discussing the number of possible solutions

How to simplify rational expressions