Answer: \(\tan\left(\dfrac{3\pi}{4}\right)=-1,\quad\)  \(\tan(210^\circ) = \dfrac{\sqrt{3}}{3},\quad\) \(\tan(\pi) = 0\)

Solution Method: To find the exact value of tangent, we use the formula
    \begin{equation*}
        \tan(\theta)=\frac{\sin{\theta}}{\cos{\theta}} 
    \end{equation*}
So we can find the exact value of tangent by finding the exact values of sine and cosine. Using right triangles, we know that every \((x,y)\) point on the unit circle is equivalent to \((\cos{\theta},\sin{\theta})\). (see previous video) So to find the exact value of tangent at a special angle, we take the x and y coordinates from the unit circle and divide them. 

For \(\tan\left(\frac{3\pi}{4}\right),\) the coordinate at \(\frac{3\pi}{4}\) is \(\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right).\) So, 
    \begin{equation*} 
        \tan(\frac{3\pi}{4})= \frac{y}{x} = \frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}} = \left(\frac{\sqrt{2}}{2}\right) \left(-\frac{2}{\sqrt{2}}\right) = -1
    \end{equation*}

For \(\tan(210^\circ),\) the coordinate is \(\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)\). So,
    \begin{equation*}
        \tan(210^\circ)= \frac{y}{x} = \frac{-\frac{1}{2}}{-\frac{\sqrt{3}}{2}} = \left( \frac{1}{2} \right) \left( \frac{2}{\sqrt{3}} \right) = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}
    \end{equation*}
We had to rationalize the fraction to get our final answer.

For \(\tan(\pi),\) \(\pi\) is a quadrantal angle located at (-1,0). So, 
    \begin{equation*}
        \tan(\pi) = \frac{y}{x} = \frac{0}{1} = 0
    \end{equation*}

Beware of Quadrantals: At the quadrantal angles \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\), the x-coordinate is 0, meaning in the tangent ratio, we are dividing by 0. Dividing by 0 means the fraction is undefined! So \(\tan\left(\frac{\pi}{2}\right)\) and \(\tan\left(\frac{3\pi}{2}\right)\) are undefined.

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 1

Answer: \(\csc\left(\dfrac{11\pi}{6}\right)=-2,\quad\) \(\sec\left(45^\circ\right)=\sqrt{2},\quad\) \(\cot\left(\dfrac{5\pi}{3}\right)=-\dfrac{\sqrt{3}}{3}\)

Solution Method: If we know the values of sine, cosine, and tangent for special angles on the unit circle, we can easily find cosecant, secant, and cotangent by taking the reciprocal of the first three functions. 
\begin{align*}
\sin{\theta} &= y \\
\cos{\theta} &= x \\
\tan{\theta} &= \frac{\sin{\theta}}{\cos{\theta}} = \frac{y}{x} \\
\csc{\theta} &= \frac{1}{y} \\
\sec{\theta} &= \frac{1}{x} \\
\cot{\theta} &= \frac{\cos{\theta}}{\sin{\theta}} = \frac{x}{y}
\end{align*}
So for \(\csc\left(\frac{11\pi}{6}\right),\) we need to find the y-coordinate at \(\frac{11\pi}{6}\) and invert it. The coordinate at \(\frac{11\pi}{6}\) is \(\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right).\) So,
    \begin{equation*}
        \csc\left(\frac{11\pi}{6}\right)=\frac{1}{y}=\frac{1}{-\frac{1}{2}} = -2
    \end{equation*}
For \(\sec(45^\circ),\) the x-coordinate at \(45^\circ\) is \(\frac{\sqrt{2}}{2}\) so
    \begin{equation*}
        \sec(45^\circ) = \frac{1}{x} = \frac{1}{\frac{\sqrt{2}}{2}} = \frac{2}{\sqrt{2}} = \frac{2\sqrt{2}}{2} = \sqrt{2}
    \end{equation*}
We had to rationalize to get the final answer.

For \(\cot\left(\frac{5\pi}{3}\right),\) the coordinate at \(\frac{5\pi}{3}\) is \(\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right).\) So,
    \begin{align*}
        \cot\left(\frac{5\pi}{3}\right) &= \frac{x}{y} \\ &= \frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}} \\&= \left( -\frac{1}{2} \right) \left( \frac{2}{\sqrt{3}} \right) \\ &= -\frac{1}{\sqrt{3}}\\ &= -\frac{\sqrt{3}}{3}
    \end{align*}
Beware of Quadrantals: Notice that because \(\cot(\theta) = \frac{x}{y},\) if the y-coordinate is 0 (like at 0 and \(\pi\)) cotangent will be undefined. 

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 2

Answer: \(\cos(5\pi)=-1,\quad\) \(\cot(480^\circ)=-\frac{\sqrt{3}}{3}\)

Solution Method: To find the trig value of an angle bigger than \(360^\circ,\) or \(2\pi\), we find its coterminal angle on the unit circle, that means between 0 and \(360^\circ\) (or 0 and \(2\pi\)). Since coterminal angles all have the same terminal side, the trig values of coterminal angles are the same. 

Coterminal Angle: Angles in standard position (with the initial side on the positive x-axis) that have a common terminal side. Coterminal angles differ by multiples of \(360^\circ\) or 2\(\pi\) in radians.
(For more info see the coterminal angles section.)

To find \(\cos(5\pi),\) we must first find the coterminal angle to \(5\pi\) in the unit circle. Since \(5\pi\) is greater than \(2\pi\), I'm going to subtract a rotation from \(5\pi\). A full rotation is 2\(\pi\), so \(5\pi-2\pi=3\pi\). So \(3\pi\) is coterminal to \(5\pi\). But \(3\pi\) is still greater than \(2\pi\). So I need to subtract another rotation until I get a value between 0 and \(2\pi\). So \(3\pi-2\pi=\pi\). So \(5\pi\) is coterminal to \(\pi\). Since \(5\pi\) and \(\pi\) are coterminal, \(\cos(5\pi)=\cos(\pi).\) The \(x\)-coordinate at \(\pi\) is -1, so \(\cos(5\pi)=-1.\)
Note: All even multiples of \(\pi\) are coterminal to \(2\pi\) and all odd multiple of \(\pi\) are coterminal to \(\pi\).

To find \(cot(480^\circ),\) we need to find the coterminal angle to \(480^\circ\) on the unit circle. In degrees, a rotation is \(360^\circ.\) So we do \(480^\circ -360^\circ=120^\circ,\) which is between 0 and 360 degrees. So \(120^\circ\) is coterminal to \(480^\circ\) and \(\cot(480^\circ=\cot (120^\circ.\) The coordinate at \(120^\circ\) is \(\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right).\) Cotangent is \(\frac{\cos{\theta}}{\sin{\theta}}=\frac{x}{y},\) so 
\begin{align*}
    \cot(480^\circ) = \frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}} = -\frac{1}{\sqrt{3}} = -\frac{\sqrt{3}}{3}
\end{align*}

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 3

Answer: \(\sin(-45^\circ)=-\dfrac{\sqrt{2}}{2}\quad\) \(\sec\left(-\dfrac{2\pi}{3}\right)=-2\)

Solution Method: To find the trig value of an angle less than 0, we find its coterminal angle on the unit circle, that means between 0 and \(360^\circ\) (or 0 and \(2\pi\)). Since coterminal angles all have the same terminal side, the trig values of coterminal angles are the same. 

Coterminal Angle: Angles in standard position (with the initial side on the positive x-axis) that have a common terminal side. Coterminal angles differ by multiples of \(360^\circ\) or 2\(\pi\) in radians.
(For more info see the coterminal angles section.)

Since we're starting with a negative angle in degrees, we're going to add a full rotation, 360 degrees, until the angle is between 0 and \(360^\circ.\) \(-45^\circ+350^\circ=315^\circ.\)
This means that \(-45^\circ\) and \(315^\circ\) are coterminal angles and \(\sin(-45^circ = \sin(315^\circ).\) The coordinate at \(315^\circ\) is \(\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right).\) Sine is equal to the \(y\)-coordinate, so \(\sin(-45^\circ)=-\frac{\sqrt{2}}{2}.\)

For \(\sec\left(-\frac{2\pi}{3}\right),\) we want to find the coterminal angle to \(-\frac{2\pi}{3}\). So we add \(2\pi\) to \(\frac{2\pi}{3}\): 
    \begin{equation*}
        -\frac{2\pi}{3} +2\pi= -\frac{2\pi}{3}+\frac{6\pi}{3} = \frac{4\pi}{3}
    \end{equation*}
So \(-\frac{2\pi}{3}\) and \(\frac{4\pi}{3}\) are coterminal and \(\sec\left(-\frac{2\pi}{3}\right)=\sec\left(\frac{4\pi}{3}\right).\) The coordinate at \(\frac{4\pi}{3}\) is \(\left(-\frac{1}{2}, -\frac{\sqrt{3}}{2}\right).\) Secant is the reciprocal of cosine and cosine is the x-coordinate, so we have
    \begin{equation*} 
        \sec\left(-\frac{2\pi}{3}\right) = \sec\left(\frac{4\pi}{3}\right) = \frac{1}{\cos{\frac{4\pi}{3}}} = \frac{1}{-\frac{1}{2}}=-2
    \end{equation*}

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 4

Answer: \(\theta = \dfrac{\pi}{3}, \dfrac{2\pi}{3}\)

Solution Method: If we recall the Unit Circle, we can solve this problem without a calculator. 

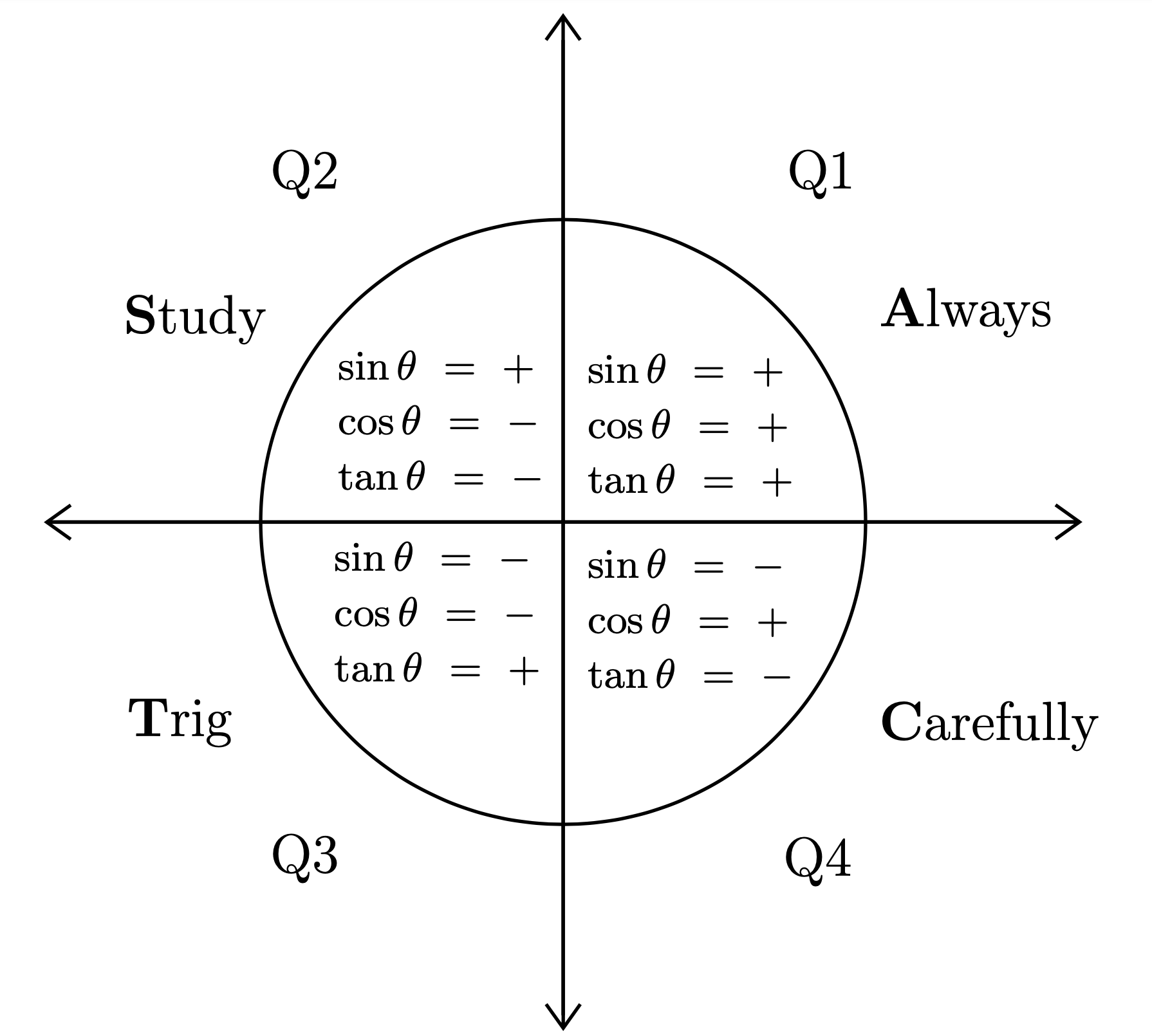First, we're going to look at the trig function and its sign. Each trig function is only positive in two quadrants on the unit circle, and negative in the other two. To help us remember which quadrants each trig function is positive in, we use the acronym ASTC, Always-Study-Trig-Carefully. You may have heard it before as All-Students-Take-Calculus or Add-Sugar-To-Coffee, use whatever works for you. In the first quadrant, all three (sin, cosine, and tangent) are positive. In the second quadrant, sine is positive and cosine and tangent are negative, in the third tangent is positive (because negative divided by negative is positive), and in the fourth quadrant cosine is positive. 
 
In this problem, we have a positive sine. So that narrows us down to angles in Q1 or Q2. 

Next, since \(\sin \theta =y,\) we need to recall if multiples of \(\frac{\pi}{6},\frac{\pi}{4},\) or \(\frac{\pi}{3}\) have y-coordinates of \(\pm\frac{\sqrt{3}}{2}\). The multiples of \(\frac{\pi}{3}\) have y-coordinates of \(\pm\frac{\sqrt{3}}{2}\).
 
So now we combine the facts that \(\theta\) is in Q1 or Q2 and a multiple of \(
    \frac{\pi}{3}\). The multiple of \(
    \frac{\pi}{3}\) in Q1 is \(
    \frac{\pi}{3}\), and the multiple in Q2 is \(
    \frac{2\pi}{3}\). 

So the \(\theta\)s in \([0,2\pi]\) satisfying \(\sin{\theta}=\frac{\sqrt{3}}{2}\), are \(\theta = 
    \frac{\pi}{3}\) and \(\theta = \frac{2\pi}{3}\).

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 5

Answer:  \(\theta=225^\circ\)

Solution Method: In this problem, we need to find \(0^\circ\) \(\leq \theta \leq\) \(360^\circ\) satisfying two conditions. First, let’s narrow down the possible quadrants for \(\theta\).

\(\tan\theta>0\) means tangent needs to be positive. Using our acronym ASTC, we know that tangent is positive in Q1 and Q3.

We also have that secant is negative. Secant is the reciprocal of cosine, so their signs will be the same. So we need cosine to be negative, which occurs in Q2 and Q3.

Now \(\theta\) has to satisfy BOTH conditions because it’s an "and" statement. So \(\theta\) can only be in Q3.

Now that we have the quadrant, we need to determine if \(\theta\) has a reference angle of \(30^\circ,\) \(45^\circ,\) or \(60^\circ.\) I don’t know the secant values on the unit circle off the top of my head, but I do know the cosine values because I know the x-coordinates. If \(\sec{\theta}=-\sqrt{2},\) \(\cos{\theta}=-\frac{1}{\sqrt{2}}=-\frac{\sqrt{2}}{2}\). Reference angles of \(45^\circ\) have x-coordinates of \(\pm\frac{\sqrt{2}}{2}\).

So then \(\theta\) is in Q3 and has a reference angle of \(45^\circ,\) so \(\theta=225^\circ\) is the only answer.

If you would like to see more videos on this topic, click the following link and check the related videos. 
Trig Functions with the Unit Circle Exercise 6