Solution: \(a=10\tan (22^\circ)=4.04\)

Solution Method: For this problem, we will use trig ratios to solve for the missing side length. 

The first step is to determine which trig ratio to use to solve the problem. To choose, we look at what is given in the triangle, and what we want to find. We are given an angle measure of \(22^\circ\) and a side length of 10. Specifically, the side of length 10 is adjacent to the angle of \(22^\circ.\) We want to find the side length of a, the side opposite the \(22^\circ.\) So we need a trig ratio that relates the opposite and adjacent side lengths of an angle: tangent. 

Now that we know to use tangent, we set up the trig ratio using the information in the problem. 
    \begin{align*}
        \tan(\theta) &= \frac{opposite}{adjacent} \\
        \tan(22^\circ) &= \frac{a}{10}
    \end{align*}
Now we have an equation we can solve for \(a.\) 
    \begin{align*}
        10\tan(22^\circ)&= a \\
        4.04 &= a
    \end{align*}
Note: When using trigonometric functions in your calculator; if the angle measure is given in degrees, make sure your calculator is in degree mode.

If you would like to see more videos on this topic, click the following link and check the related videos. 
Solving Problems with Trig Exercise 1

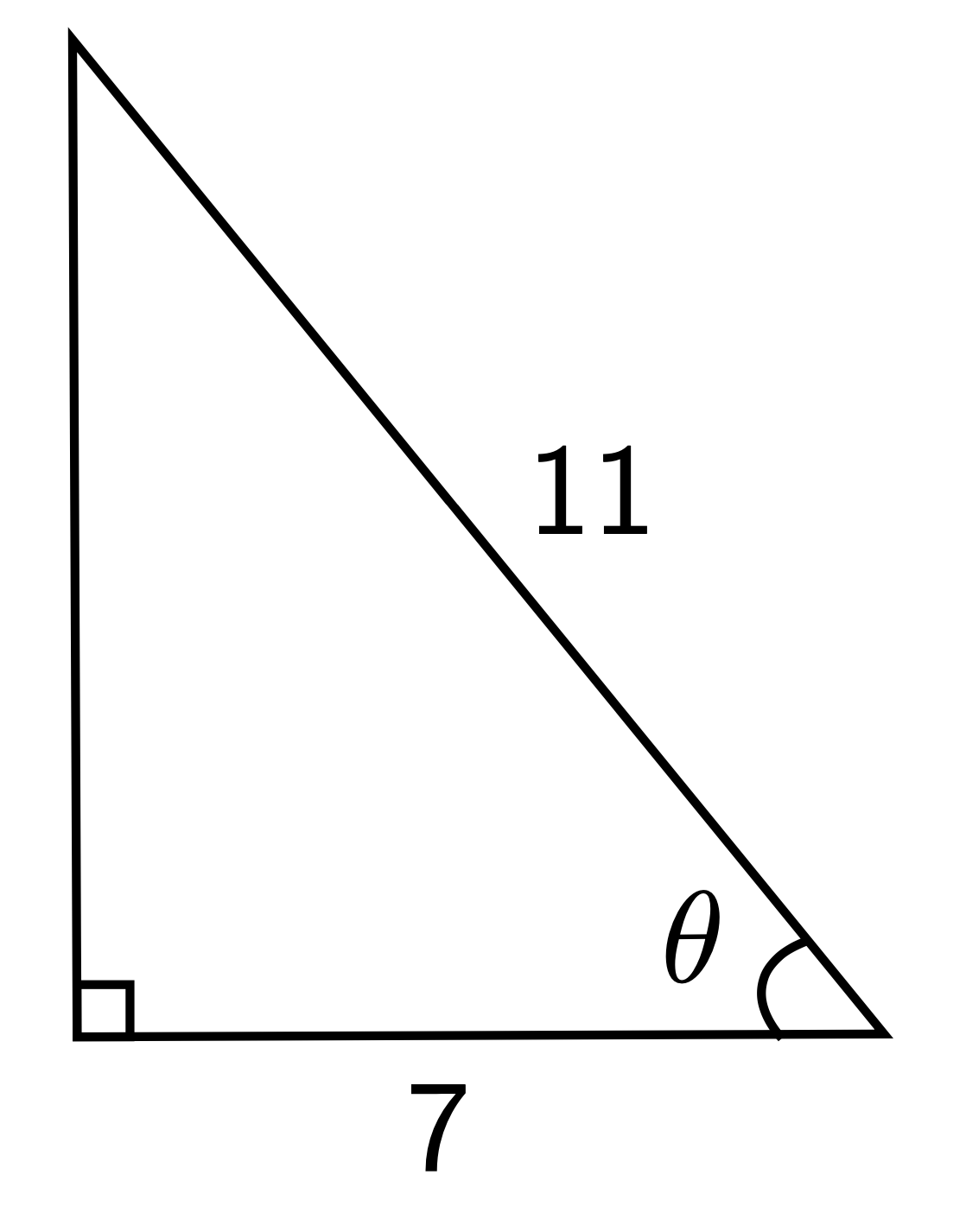
Solution: \(\theta=\cos^{-1}\left(\dfrac{7}{11}\right)=50.5^\circ\)

Solution Method: In this problem, we will use an inverse trigonometric function to solve for the missing angle measure. 

Our first step is to determine which trig function to use. We are given that the side adjacent to angle \(\theta\) has length 7, and the hypotenuse has length 11. Thus, we need a trig ratio that relates adjacent and hypotenuse side lengths (think SOHCAHTOA): cosine. 

Now, we set up the trig ratio with the values given in the problem.
\begin{equation}
    \cos(\theta) = \frac{adjacent}{hypotenuse} = \frac{7}{11}
\end{equation}

To solve for an angle measure, given a trig ratio, we need inverse trigonometric functions. A trig function takes an angle measure and outputs a ratio of side lengths. Thus, an inverse trig function takes a side length ratio and outputs an angle measure. Mathematically, the six inverse functions are defined:
Furthermore, each inverse trig function "undoes" its respective trig function. 

So, to finish the problem above, we apply inverse cosine to both sides of equation (1),
        \begin{align*}
            \cos^{-1}\left(\cos(\theta)\right) &= \cos^{-1}\left(\frac{7}{11}\right) \\
            \theta &= \cos^{-1}\left(\frac{7}{11}\right) \\
            \theta &= 50.5^\circ
        \end{align*}
Note 1: When using an inverse trig function in the calculator, your output will only be in degrees if you are in degree mode.

Note 2: The \(^{-1}\) notation for an inverse trig function is not to be confused for an exponent. This is why the reciprocals of trig functions have their own names. Another notation for inverse trig functions is "arc_____". E.g. "\(\sin^{-1}()\)" and "arcsin()" are both used as inverse sine.

If you would like to see more videos on this topic, click the following link and check the related videos. 
Solving Problems with Trig Exercise 2